TreeSet 是 Java 集合框架中 Set 接口的实现类,它基于红黑树(Red-Black Tree)数据结构来存储元素,具有排序和去重的特性。
什么是红黑树?
红黑树是一种自平衡的二叉查找树,是一种高效的查找树。它是由 Rudolf Bayer 于1972年发明,在当时被称为对称二叉 B 树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树。
红黑树具有良好的效率,它可在 O(logN) 时间内完成查找、增加、删除等操作。因此,红黑树在业界应用很广泛,比如 Java 中的 TreeMap,JDK 1.8 中的 HashMap 中的 map 均是基于红黑树结构实现的。
我们要知道二叉搜索树,在不为空的情况下,左子树上所有结点的值均小于它的根结点的值,右子树上所有结点的值均大于它的根结点的值。它使得数据查找起来不是线性查找(O(n)),平均复杂度仅仅为O(log(n))。如下图:
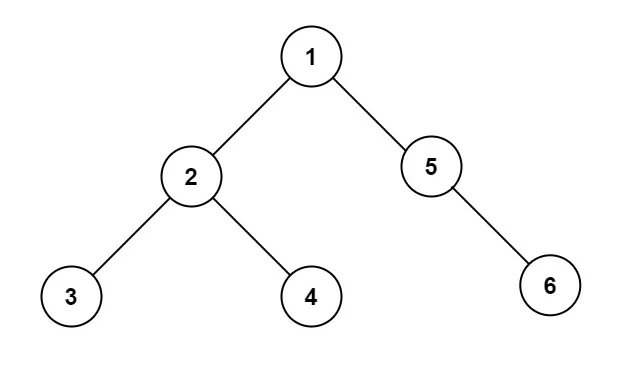
但是在最坏情况下(数据有顺序,如 1,2,3,4,5,6),二叉搜索树可能变为线性搜索,退化为链表,复杂度为 O(n)。如下图:
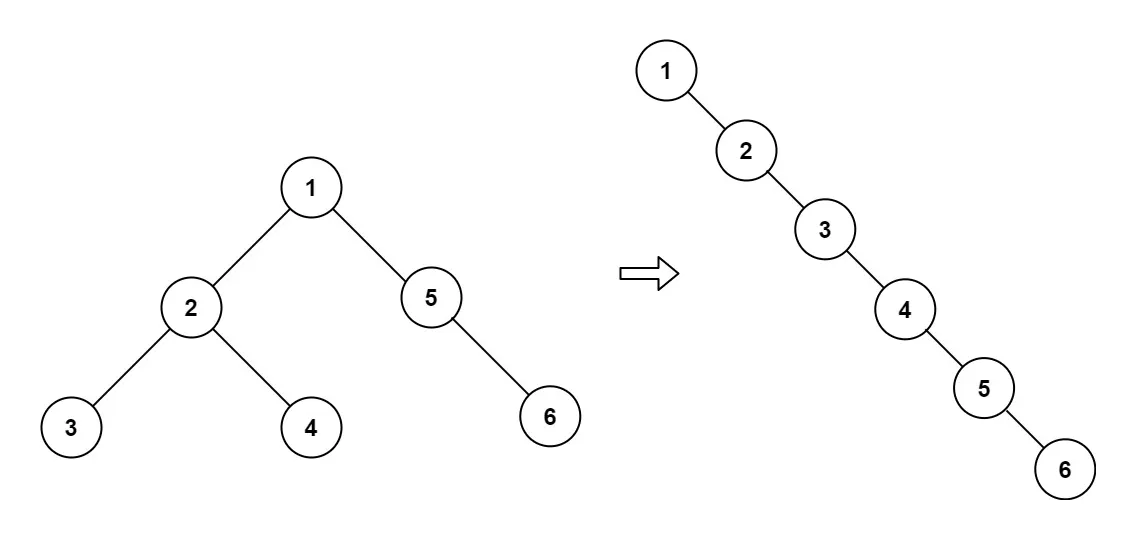
为了避免这种情况发生,就到了我们的主角红黑树,它规定了一些性质使得这种情况不会发生。
红黑树主要有这五条性质:
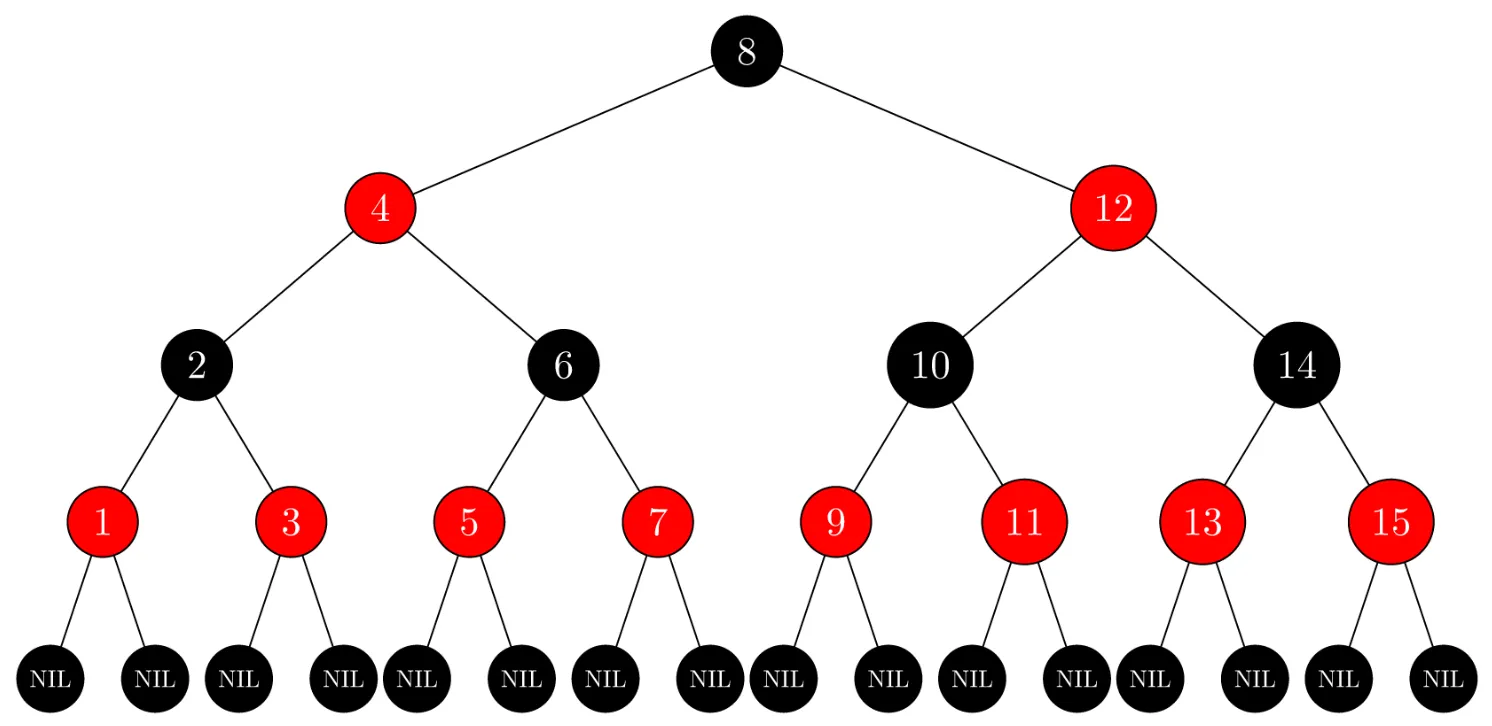
红黑树的优点如下:
高效的平衡性:红黑树通过严格的着色规则(每个节点非红即黑)和旋转操作(左旋、右旋),确保树的高度始终保持在 O(log n) 级别(n 为节点数)。这使得查找、插入、删除等操作的时间复杂度稳定在 O(log n),避免了普通二叉搜索树在最坏情况下(如有序插入)退化为链表(O (n) 复杂度)的问题。
较少的旋转操作:相比其他自平衡树(如 AVL 树),红黑树维持平衡时所需的旋转次数更少。AVL 树要求左右子树高度差不超过 1,可能导致频繁旋转;而红黑树的平衡条件更宽松,插入时最多需要 2 次旋转,删除时最多需要 3 次旋转,实际性能更优。
内存占用低:红黑树每个节点只需存储一个额外的颜色标记(红或黑),空间开销小。而 AVL 树需要存储平衡因子(或高度),内存占用相对更高。
适合频繁插入删除的场景:由于旋转操作少,红黑树在动态数据(频繁插入、删除)场景下表现更高效,常用于实现关联容器(如 Java 的 TreeMap、TreeSet 等)。
红黑树的缺点如下:
实现复杂:红黑树的插入和删除逻辑涉及多种情况判断(如 uncle 节点颜色、旋转方向等),代码实现较为繁琐,容易出错。相比之下,普通二叉搜索树或哈希表的实现更简单。
查询性能略逊于 AVL 树:红黑树最坏情况下的高度为 2log(n+1),而 AVL 树是严格的平衡树(高度约为 1.44log (n+2)-1.328)。在纯查询场景下,AVL 树的查找效率理论上更高,但实际应用中差异不明显。
不适合静态数据:对于极少修改(插入 / 删除)的静态数据,红黑树的平衡机制带来的开销显得多余。此时,有序数组 + 二分查找可能更高效。
关于更多红黑树的知识请参考专业的数据结构书籍。
java 广告位
TreeSet 核心特性
有序性
TreeSet 中的元素将按照自然顺序或自定义比较器进行排序,其中:
自然排序
TreeSet 中的元素类需实现 Comparable 接口,并重写 compareTo() 方法,例如:
package com.hxstrive.java_collection;
import java.util.Set;
import java.util.TreeSet;
public class Demo {
static class Student implements Comparable<Student> {
private String name;
private int age;
public Student(String name, int age) {
this.name = name;
this.age = age;
}
// 看这里
@Override
public int compareTo(Student o) {
// 按年龄升序排序
return Integer.compare(this.age, o.age);
}
@Override
public String toString() {
return "Student{" +
"name='" + name + '\'' +
", age=" + age +
'}';
}
}
public static void main(String[] args) {
Set<Student> set = new TreeSet<>();
set.add(new Student("Alice", 20));
set.add(new Student("Bob", 18));
set.add(new Student("Helen", 32));
for(Student student : set) {
System.out.println(student);
}
//输出:
//Student{name='Bob', age=18}
//Student{name='Alice', age=20}
//Student{name='Helen', age=32}
}
}
定制排序
创建 TreeSet 时传入自定义的 Comparator 比较器对象,实现自定义排序,例如:
package com.hxstrive.java_collection;
import java.util.Comparator;
import java.util.Set;
import java.util.TreeSet;
public class Demo {
static class Student {
private String name;
private int age;
public Student(String name, int age) {
this.name = name;
this.age = age;
}
@Override
public String toString() {
return "Student{" +
"name='" + name + '\'' +
", age=" + age +
'}';
}
}
public static void main(String[] args) {
Set<Student> set = new TreeSet<>(new Comparator<Student>() {
@Override
public int compare(Student o1, Student o2) {
return Integer.compare(o1.age, o2.age);
}
});
set.add(new Student("Alice", 20));
set.add(new Student("Bob", 18));
set.add(new Student("Helen", 32));
for(Student student : set) {
System.out.println(student);
}
//输出:
//Student{name='Bob', age=18}
//Student{name='Alice', age=20}
//Student{name='Helen', age=32}
}
}
唯一性
TreeSet 中不会允许存在重复元素,其判断依据并非简单的 equals() 方法,而是通过比较器(Comparator)或元素自身的自然排序(Comparable)来实现的。
TreeSet 判断两个元素是否重复的核心规则是:如果两个元素比较的结果为 0(即 compareTo() 或 compare() 方法返回 0),则认为它们是重复元素,后添加的元素会被拒绝。
如果使用自然排序(元素实现 Comparable 接口),则通过 element1.compareTo(element2) == 0 判断重复。
如果使用定制排序(传入 Comparator),则通过 comparator.compare(element1, element2) == 0 判断重复。
注意:TreeSet 的唯一性判断不直接依赖 equals() 方法,但根据 Java 规范,通常建议:如果 compareTo() 返回 0,则 equals() 也应返回 true(反之亦然),以保证集合行为的一致性。如果违反这一规范(例如 compareTo() 返回 0 但 equals() 返回 false),TreeSet 会将它们视为重复元素(拒绝添加),但可能导致与其他集合(如 HashSet)的行为不一致。
无索引
不能通过索引访问元素,这是因为底层采用红黑树数据结构实现决定的。若要支持 get(index),需要从根节点开始依次遍历计数(类似链表的“下标访问”),时间复杂度为 O(n),违背了 TreeSet 追求高效操作(O (log n))的设计目标。
非同步
线程不安全,在多线程环境下,需要手动处理同步问题。实际开发中,需根据并发程度选择合适的线程安全方案:低并发可用同步包装类,高并发推荐使用 ConcurrentSkipListSet。
查询效率高
TreeSet 具有高效的查询性能,源于其底层基于红黑树(一种自平衡二叉搜索树)的数据结构设计,使得基本查询操作的时间复杂度稳定在 O(log n)(n 为元素数量),远优于线性结构(如链表的 O(n))。
TreeSet 常用方法
除了 Set 接口的基本方法外,TreeSet 还提供了导航相关的方法,如下:
ceiling(E e) 返回此集合中大于等于指定元素 e 的最小元素。若存在满足条件的元素,则返回该元素;若不存在(即集合中所有元素都小于 e),则返回 null。
floor(E e) 返回此集合中小于等于指定元素 e 的最大元素。若存在满足条件的元素,则返回该元素;若不存在(即集合中所有元素都大于 e),则返回 null。
higher(E e) 返回此集合中严格大于指定元素 e 的最小元素。若存在满足条件的元素,则返回该元素;若不存在(即集合中所有元素都小于等于 e),则返回 null。
lower(E e) 返回此集合中严格小于指定元素 e 的最大元素。若存在满足条件的元素,则返回该元素;若不存在(即集合中所有元素都大于等于 e),则返回 null。
subSet(E fromElement, E toElement) 返回此集合中元素范围在 [fromElement, toElement)(左闭右开)的子集合。注意,子集合是原集合的视图,对原集合的修改会影响子集合,反之亦然;若 fromElement 大于 toElement,会抛出 IllegalArgumentException 异常。
first() 返回此集合中的第一个(最小的)元素。若集合为空,抛出 NoSuchElementException
last() 返回此集合中的最后一个(最大的)元素。若集合为空,抛出 NoSuchElementException
pollFirst() 移除并返回此集合中的第一个(最小的)元素。若集合为空,返回 null
pollLast() 移除并返回此集合中的最后一个(最大的)元素。若集合为空,返回 null
TreeSet 简单示例
下面是一个 TreeSet 的简单示例,展示了其常用方法的用法,包括添加元素、遍历、查找、范围操作等:
package com.hxstrive.java_collection.treeSet;
import java.util.TreeSet;
import java.util.Iterator;
public class TreeSetDemo {
public static void main(String[] args) {
// 1. 创建 TreeSet(默认自然排序,字符串按字典顺序)
TreeSet<String> fruits = new TreeSet<>();
// 2. 添加元素(add() 方法)
fruits.add("apple");
fruits.add("banana");
fruits.add("orange");
fruits.add("grape");
fruits.add("apple"); // 重复元素,不会被添加
System.out.println("TreeSet 中的元素: " + fruits);
// 3. 基本操作
System.out.println("集合大小: " + fruits.size());
System.out.println("是否包含 'banana': " + fruits.contains("banana"));
// 4. 遍历元素
System.out.println("\n使用迭代器遍历:");
Iterator<String> iterator = fruits.iterator();
while (iterator.hasNext()) {
System.out.println(iterator.next());
}
// 5. 导航方法
System.out.println("\n第一个元素: " + fruits.first());
System.out.println("最后一个元素: " + fruits.last());
System.out.println("小于 'orange' 的最大元素: " + fruits.lower("orange"));
System.out.println("大于 'orange' 的最小元素: " + fruits.higher("orange"));
System.out.println("大于等于 'grape' 的最小元素: " + fruits.ceiling("grape"));
System.out.println("小于等于 'grape' 的最大元素: " + fruits.floor("grape"));
// 6. 范围操作
System.out.println("\n从 'banana' 到 'orange' 的子集合: " +
fruits.subSet("banana", "orange")); // 左闭右开
// 7. 删除元素
fruits.remove("banana");
System.out.println("删除 'banana' 后的集合: " + fruits);
// 8. 移除并返回首尾元素
String firstRemoved = fruits.pollFirst();
String lastRemoved = fruits.pollLast();
System.out.println("移除的第一个元素: " + firstRemoved);
System.out.println("移除的最后一个元素: " + lastRemoved);
System.out.println("操作后的集合: " + fruits);
// 9. 清空集合
fruits.clear();
System.out.println("清空集合后是否为空: " + fruits.isEmpty());
}
}
运行结果:
TreeSet 中的元素: [apple, banana, grape, orange]
集合大小: 4
是否包含 'banana': true
使用迭代器遍历:
apple
banana
grape
orange
第一个元素: apple
最后一个元素: orange
小于 'orange' 的最大元素: grape
大于 'orange' 的最小元素: null
大于等于 'grape' 的最小元素: grape
小于等于 'grape' 的最大元素: grape
从 'banana' 到 'orange' 的子集合: [banana, grape]
删除 'banana' 后的集合: [apple, grape, orange]
移除的第一个元素: apple
移除的最后一个元素: orange
操作后的集合: [grape]
清空集合后是否为空: true
java 广告位
TreeSet 内部维护了一个 TreeMap 实例,元素存储在 TreeMap 的 key 位置,value 则使用一个固定的 PRESENT 对象占位,源码如下:
public class TreeSet<E> extends AbstractSet<E>
implements NavigableSet<E>, Cloneable, java.io.Serializable {
// 使用 NavigableMap 存储元素,TreeSet 的元素作为 map 的 key,
// value 固定为 PRESENT 对象。这是 TreeSet 依赖 TreeMap 实现的核心体现。
private transient NavigableMap<E,Object> m;
// 用于填充底层 map 的 value 的占位对象,所有元素共享同一个 PRESENT 实例
// 这样设计是为了节省内存,因为 TreeSet 只需要用到 map 的 key 来存储元素
private static final Object PRESENT = new Object();
/**
* 创建一个由指定 NavigableMap 支持的 TreeSet
* 主要用于 TreeSet 内部或同包类(如 TreeMap)创建实例时使用
*
* @param m 作为底层存储的 NavigableMap 实例
*/
TreeSet(NavigableMap<E,Object> m) {
this.m = m;
}
/**
* 创建一个空的 TreeSet,元素按照自然顺序排序
*
* 注意事项:
* 1. 所有添加到集合中的元素必须实现 Comparable 接口
* 2. 元素之间必须可相互比较(e1.compareTo(e2) 不能抛出 ClassCastException)
* 3. 若添加不满足上述条件的元素,add 方法会抛出 ClassCastException
*/
public TreeSet() {
// 初始化底层为 TreeMap(默认自然排序),并将其传递给私有构造方法
this(new TreeMap<>());
}
/**
* 创建一个空的 TreeSet,使用指定的比较器进行排序
*
* @param comparator 用于排序的比较器,若为 null 则使用元素的自然排序
*
* 注意事项:
* 1. 所有添加的元素必须能被指定比较器处理(不会抛出 ClassCastException)
* 2. 若添加不兼容的元素,add 方法会抛出 ClassCastException
*/
public TreeSet(Comparator<? super E> comparator) {
// 初始化底层为带指定比较器的 TreeMap
this(new TreeMap<>(comparator));
}
/**
* 创建一个包含指定集合中所有元素的 TreeSet,元素按自然顺序排序
*
* @param c 包含初始元素的集合
*
* 注意事项:
* 1. 集合 c 中的元素必须实现 Comparable 接口且可相互比较
* 2. 若元素不满足上述条件,会抛出 ClassCastException
* 3. 若指定集合为 null,会抛出 NullPointerException
*/
public TreeSet(Collection<? extends E> c) {
// 先调用无参构造初始化底层 TreeMap(自然排序)
this();
// 将集合 c 中的所有元素添加到当前 TreeSet 中
addAll(c);
}
/**
* 创建一个包含指定有序集合中所有元素的 TreeSet,使用与原集合相同的排序规则
*
* @param s 提供初始元素和排序规则的有序集合
*
* 注意事项:
* 1. 新集合会复用原有序集合的比较器(若原集合使用自然排序,则新集合也一样)
* 2. 若指定有序集合为 null,会抛出 NullPointerException
*/
public TreeSet(SortedSet<E> s) {
// 使用原有序集合的比较器初始化底层 TreeMap
this(s.comparator());
// 将原有序集合中的所有元素添加到当前 TreeSet 中
addAll(s);
}
// ...省略...
}
注意,上面简单示例中用到的很多方法实现均是调用底层 TreeMap 的方法进行实现,源码如下:
public Comparator<? super E> comparator() {
return m.comparator();
}
public E first() {
return m.firstKey();
}
public E last() {
return m.lastKey();
}
public E lower(E e) {
return m.lowerKey(e);
}
public E floor(E e) {
return m.floorKey(e);
}
public E ceiling(E e) {
return m.ceilingKey(e);
}
public E higher(E e) {
return m.higherKey(e);
}
public E pollFirst() {
Map.Entry<E,?> e = m.pollFirstEntry();
return (e == null) ? null : e.getKey();
}
public E pollLast() {
Map.Entry<E,?> e = m.pollLastEntry();
return (e == null) ? null : e.getKey();
}
更多详细信息请参考 https://docs.oracle.com/javase/8/docs/api/java/util/TreeSet.html API 文档。




